Extra Credit!

December 7, 2023

The purpose of this assignment is to allow students to demonstrate their understanding of various abstract and applied physics topics. Because of the nature of this assignment, it will be graded fairly strictly--pay close attention to the Notes below. Assignments which are not completed as required will not be evaluated.

NOTES:

1) The Extra Credit Assignment consists of up to three problems, to be completed outside of class.

2) This assignment is Extra Credit and is not required.

3) This assignment is intended to provide students with the opportunity to review and practice again some of the material we've covered, and not all students need the same amount of review or extra practice. 
     (Remembering that you've all had one extra credit question already this semester...)
     If your current test average in the course (not your overall average but your test average) is 79% or less (as of January 1 (that is, everything up to and including the rotational motion unit test), you may attempt all THREE problems.
     If your current test average is between 80% and 89%, you may attempt problems 2-3. 
     If your current test average is above 90% or above, you may do only problem 3.  

4) The total points earned by a student on this assignment will be determined by the instructor based on a number of factors, including number of problems completed, difficulty of problem, and overall quality of assignments submitted by students.

5) You may work on the problems with other people--in fact, this is encouraged--but each person must write up and complete his or her own assignment to be turned in. Even when numeric answers to problems are the same, solutions from each student must be written independently, and differently, and developed and explained in each student's own words.

6) The assignment must have a separate COVER SHEET that includes your Name, Date, Course, Period, and Name of Assignment. Additionally, a statement of your TEST AVERAGE and a listing of the problems you have attempted must be included on the cover sheet. Staple this cover sheet to the front of the problems that you've solved.

7) Each response must be written on a separate piece of paper, which must include: 
         a) The problem number at the top of the page.
         b) The original question written out in full (I'd suggest you cut and paste from this document).
         c) Your solution, hand-written, with all work shown in detail.
         d) Drawings, diagrams, or graphs with labels may (and should!) be used to explain your solution more clearly.
         e) Written explanations (blurbs, in English) explaining important steps in your solution.
         f) The final answer, with a box around it.

If this seems like an awful lot of work, it is! Remember that this is Extra Credit--you are trying to impress the instructor with how well you can think. If in doubt, do a little more than you believe you should, rather than trying to get by with less and losing points in the process.

8 ) The instructor will be available to answer questions about the assignment on a limited basis before school, after school, and possibly by e-mail. The instructor will not be able to help you if you leave all of your work until the night before the assignment is due.

9 ) Your completed assignment must be turned in directly to the instructor anytime before 3:15 pm on Tuesday, Jaunary 9 (this is in the second week after the break, and three days before the end of the second semester).  

EXAMPLE PROBLEM AND SOLUTION:

SAMPLE PROBLEM:

In "The Matrix," Neo is given a test by Morpheus, who asks him to leap from the top of one building to another. Assume the buildings are each 100m tall, and 15m apart. Neo runs and leaps from the first building with a velocity of 5.00 m/s at an angle of 36.9 degrees (toward the second building).

a. Will he make it to the next building?
b. Where exactly will Neo land?

(Assume no air friction in this problem.)

SOLUTION (Note that the written comments here are examples of "blurbs" that you will also be including in your solutions!):

a) This is a projectile problem, so we'll need to solve it by considering the x and y situations separately. The first thing we should do is split Neo's initial velocity into horizontal and vertical components.

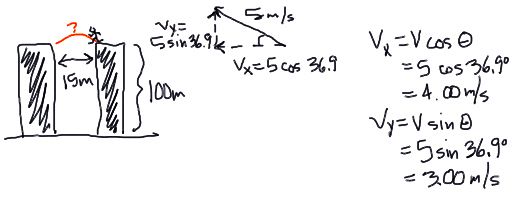
As Neo flies through the air, his horizontal velocity of 4.00 m/s remains constant--there is no horizontal force that causes him to accelerate in this direction. In the vertical direction, however, gravity will cause him to accelerate down.

To find out if he makes it to the next building, we can first determine how long it will take him to travel the horizontal 15m distance between the buildings:

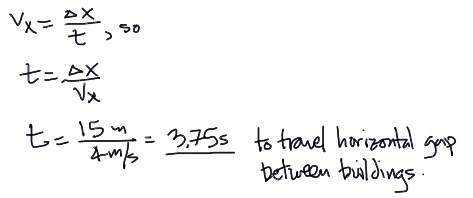
Now we can ask ourselves how long it will take Neo to return to the vertical level from which he jumped--this is the level of the second building that he needs to land on.

Therefore, Neo has only 0.61 seconds of time (calculated vertically) to travel the 15 meters between the buildings, but he needs 3.75 seconds to travel that distance. He does not make it to the next building.

b) To find where he does land, we can ask where he is vertically when he has taken 3.75 seconds to cross the horizontal gap:

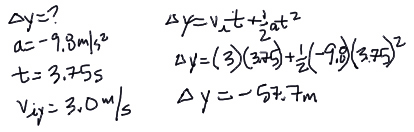
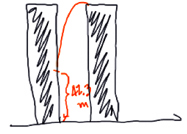
Therefore, Neo doesn't fall all the way to the ground, at least not right away. His first contact after leaving the first building is when he runs into the second building, at a distance of 57.7m below the top of the buildings, or 42.3m above the ground (see diagram below).

PROBLEMS!

1. See John jump . . .

In "the real world" (a_gravity = 9.8 m/s², down), John (mass 90 kg) can jump straight up into the air to a maximum height of .4 meters (that is, his center of mass rises .4 meters max when he jumps). Ignoring air friction:

a.) How much energy did John personally burn in making the jump to his maximum height? (What was his potential energy change?)

b.) If his legs flexed a distance .15 meters in making the jump, what was the average force his legs exerted in making the jump? (Think about how much work he did in making the jump.)

c.) What average acceleration would he have experienced during the lift-off part of the jump (i.e., while his legs were engaged)? (thnk NSL?)

d.) If John had gone to the moon where the acceleration of gravity is 1/6 that of gravity on earth, and if he expended the same amount of energy in making a jump, how high would he have gone? (fly, bird, fly)

2. See Katie Roll . . .

Kate, a roller-skater, free-rolls through a semi-circular hairpin turn of radius R. Assume that the coefficient of static friction between her skates and the pavement is known. It makes sense that if the radius of her arc is large, her MAXIMUM speed through the curve will be greater than if the radius had been small. On the other hand, it also makes sense that the larger the radius, the farther she will have to go to get through the entire curve. So the question arises, "Given there are several lanes to choose from, is there an optimal lane through which the added speed (due to a larger radius) will overcome the additional distance required to get through the curve?" In other words, in which lane will Katie make the fastest transit? To answer this, assume you have a group of skaters all racing in different lanes through the semi-circular curve. Assume the inside lane's number is designated 0 with a radius of R, the next lane's number is designated 1 with a radius of R+1, the next lane's number is designated 2 with a radius of R+2, and the nth lane's number is designated n with a radius of R+n. With all of this in mind:

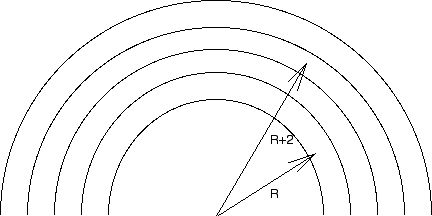a.) In terms of the known coefficient of static friction, g, R, and n, derive an expression for the maximum speed the skater in the (R+n)th lane can achieve.

b.) In terms of the coefficient of static friction, g, R, and n, derive an expression for the amount of time it will take the skater in the (R+n)th lane to get through the entire semi-circular curve.

c.) From your results, in which lane will Katie make it through the curve the fastest?

d.) After Katie determines the best run, she decides to do a run, just for fun. Choosing the outside track, she gets her tiny 55 kg frame up to 12 m/s while in the turn, then just as she is leaving the arc runs straight into her baby brother (at 145 kg) who is also on roller skates. The collision is perfectly inelastic. a.) After the collision, how fast are the two of them moving? And b.) What percentage of energy (kinetic) was lost during the collision?    

3. May Pole on Ice

Before the Soviet Union decided to make May 1 its National Arms Day, the United States celebrated that date in commemoration of spring. The day was named "May Day." During May Day, a tall pole called a "May Pole" had streamers attached to its top and was planted in the ground. In a festive spirit, kids would clutch the free end of the streamers, then prominade around and around the pole. In doing so, the streamers would overlay on one another as they wound up around the pole. The following problem is dedicated to both May Day and the lowly May Pole. A May Pole of negligible diameter was planted in the middle of a frictionless ice pond. Unfortunately, the goof-ball who made the pole attached only ONE streamer to it, and that streamer (length 3.5 meters) was not attached at the top but, rather, 1.5 meters above the ground. Realizing that she had messed up, the pole-maker tried to cover the goof by suggesting a new tradition. "Let's have someone on ice-skates skate in from the side, grab the outstretched streamer (someone would have to hold the stream taught in the beginning) and, once grabbed, move in a glide as the streamer wound around the pole with ever diminishing radius." Everyone said, "Oh, goody, a game," and started to play. The first skater (m = 100 kg) approached the streamer from the side going 5 m/s (see sketch looking from above). He grabbed the streamer, stopped pumping (that is, he stopped pushing to make himself go faster), and simply held on as he and the streamer proceeds around and around the pole. (Again, see sketches.)

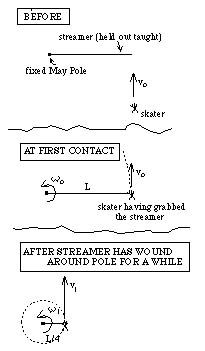a.) In "flash from the past" mode, how large a force must the streamer exert on the 100 kg skater to pull him into circular motion just after he grabs it?

b.) JUST A MOMENT AFTER the skater grasps the streamer and begins to move in a circular path around the pole, what is his angular velocity?

c.) The streamer is rigidly attached to the pole (that is, it isn't sliding around the pole), so as the skater and streamer wind around the pole, the streamer's pole-to-end length diminishes and the skater speeds up in the process (remember, he is just gliding--he isn't pushing to increase his speed). This increase of the skater's speed is the consequence of what principle? (Only a few words are needed here.)

d.) What will the skater's angular speed be when the distance between the pole and the streamer is only 2 meters?

e.) Is energy conserved as the skater moves from the 3.5 radius circle to the 2 meter circle. (Actually calculate the amount of energy in the two situations and compare them.)

f.) Take a shot at explaining the result you got in Part e. That is, if there is a disparity in energy, from whence did the energy go or come?